Exercise 5 - Distance To

In poorly designed 2D games, players might be moving diagonally at a speed of 1.414 times faster than they would horizontally or vertically.

To prove that a diagonal point on a 2D grid is a longer distance than a vertical or horizontal point, an algorithm is needed to calculate the distance between two points. This algorithm can be generated from a distance formula derived from Pythagorean theorem:

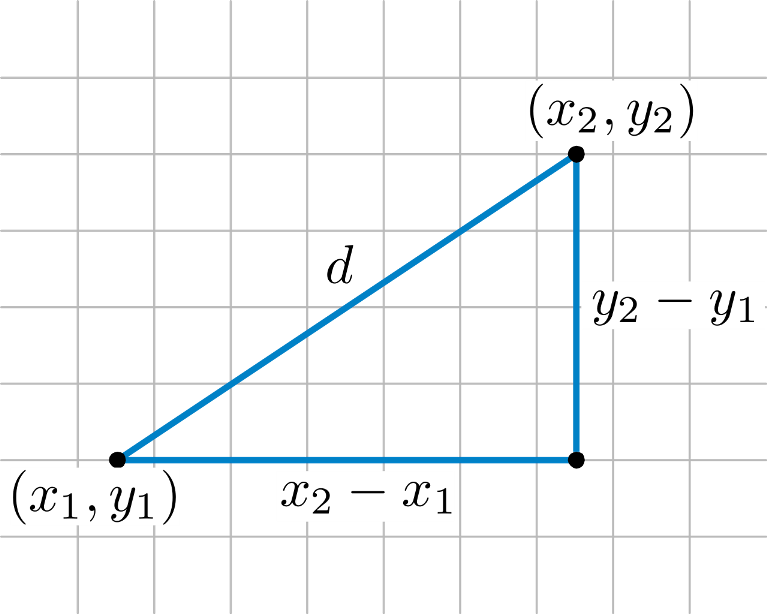
The formula for distance between the two points (x1, y1) and (x2, y2) is:

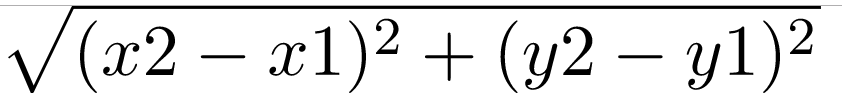
Can you write an algorithm and Python code module to achieve this? Hint: The formula above can be written in pseudocode as follows:

SQRT((X2 - X1)^2 + (Y2 - Y1)^2)

BEGIN calculateDistance(X1,Y1,X2,Y2)
  ...
END

BEGIN
  ...
END

Code the calculateDistance module you have planned above in Python, using the supplied function call parameter values to test the accuracy answer:

import math
#def ...
  #return ...

result = calculateDistance(1,1,2,2)
print(result) #1.4142135623730951

Run Code